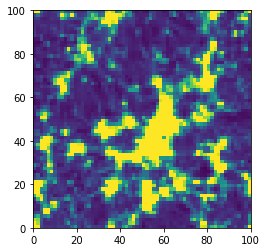
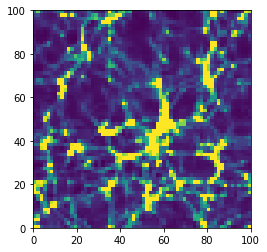
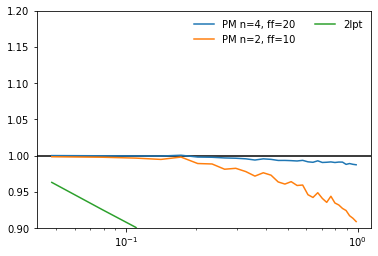
Running with 5 steps, ff=2...
--- stepping t=0.14215686274509803, i=2097152
--- stepping t=0.38725490196078427, i=2097152
--- stepping t=0.6323529411764706, i=2097152
--- stepping t=0.8774509803921569, i=2097152
Running with 10 steps, ff=2...
--- stepping t=0.07407407407407407, i=2097152
--- stepping t=0.1830065359477124, i=2097152
--- stepping t=0.29193899782135074, i=2097152
--- stepping t=0.40087145969498905, i=2097152
--- stepping t=0.5098039215686274, i=2097152
--- stepping t=0.6187363834422658, i=2097152
--- stepping t=0.7276688453159041, i=2097152
--- stepping t=0.8366013071895424, i=2097152
--- stepping t=0.9455337690631808, i=2097152
Running with 20 steps, ff=2...
--- stepping t=0.04540763673890609, i=2097152
--- stepping t=0.09700722394220845, i=2097152
--- stepping t=0.14860681114551083, i=2097152
--- stepping t=0.2002063983488132, i=2097152
--- stepping t=0.2518059855521156, i=2097152
--- stepping t=0.30340557275541796, i=2097152
--- stepping t=0.3550051599587203, i=2097152
--- stepping t=0.40660474716202266, i=2097152
--- stepping t=0.45820433436532504, i=2097152
--- stepping t=0.5098039215686274, i=2097152
--- stepping t=0.5614035087719298, i=2097152
--- stepping t=0.6130030959752322, i=2097152
--- stepping t=0.6646026831785345, i=2097152
--- stepping t=0.7162022703818369, i=2097152
--- stepping t=0.7678018575851393, i=2097152
--- stepping t=0.8194014447884417, i=2097152
--- stepping t=0.8710010319917441, i=2097152
--- stepping t=0.9226006191950464, i=2097152
--- stepping t=0.9742002063983487, i=2097152
Running with 40 steps, ff=2...
--- stepping t=0.03217697335344394, i=2097152
--- stepping t=0.05731523378582202, i=2097152
--- stepping t=0.0824534942182001, i=2097152
--- stepping t=0.10759175465057817, i=2097152
--- stepping t=0.13273001508295626, i=2097152
--- stepping t=0.15786827551533433, i=2097152
--- stepping t=0.1830065359477124, i=2097152
--- stepping t=0.20814479638009048, i=2097152
--- stepping t=0.23328305681246855, i=2097152
--- stepping t=0.2584213172448466, i=2097152
--- stepping t=0.28355957767722473, i=2097152
--- stepping t=0.3086978381096028, i=2097152
--- stepping t=0.3338360985419809, i=2097152
--- stepping t=0.3589743589743589, i=2097152
--- stepping t=0.384112619406737, i=2097152
--- stepping t=0.40925087983911507, i=2097152
--- stepping t=0.43438914027149317, i=2097152
--- stepping t=0.45952740070387127, i=2097152
--- stepping t=0.4846656611362493, i=2097152
--- stepping t=0.5098039215686274, i=2097152
--- stepping t=0.5349421820010055, i=2097152
--- stepping t=0.5600804424333835, i=2097152
--- stepping t=0.5852187028657616, i=2097152
--- stepping t=0.6103569632981397, i=2097152
--- stepping t=0.6354952237305178, i=2097152
--- stepping t=0.6606334841628959, i=2097152
--- stepping t=0.6857717445952739, i=2097152
--- stepping t=0.710910005027652, i=2097152
--- stepping t=0.7360482654600301, i=2097152
--- stepping t=0.7611865258924082, i=2097152
--- stepping t=0.7863247863247862, i=2097152
--- stepping t=0.8114630467571643, i=2097152
--- stepping t=0.8366013071895424, i=2097152
--- stepping t=0.8617395676219205, i=2097152
--- stepping t=0.8868778280542986, i=2097152
--- stepping t=0.9120160884866766, i=2097152
--- stepping t=0.9371543489190547, i=2097152
--- stepping t=0.9622926093514328, i=2097152
--- stepping t=0.9874308697838109, i=2097152
Running with 80 steps, ff=2...
--- stepping t=0.025812856788284932, i=2097152
--- stepping t=0.038222884090344994, i=2097152
--- stepping t=0.05063291139240506, i=2097152
--- stepping t=0.06304293869446512, i=2097152
--- stepping t=0.07545296599652519, i=2097152
--- stepping t=0.08786299329858525, i=2097152
--- stepping t=0.10027302060064532, i=2097152
--- stepping t=0.11268304790270538, i=2097152
--- stepping t=0.12509307520476545, i=2097152
--- stepping t=0.13750310250682551, i=2097152
--- stepping t=0.14991312980888558, i=2097152
--- stepping t=0.16232315711094564, i=2097152
--- stepping t=0.1747331844130057, i=2097152
--- stepping t=0.18714321171506576, i=2097152
--- stepping t=0.19955323901712582, i=2097152
--- stepping t=0.21196326631918588, i=2097152
--- stepping t=0.22437329362124595, i=2097152
--- stepping t=0.236783320923306, i=2097152
--- stepping t=0.24919334822536607, i=2097152
--- stepping t=0.26160337552742613, i=2097152
--- stepping t=0.2740134028294862, i=2097152
--- stepping t=0.28642343013154625, i=2097152
--- stepping t=0.29883345743360634, i=2097152
--- stepping t=0.3112434847356664, i=2097152
--- stepping t=0.32365351203772647, i=2097152
--- stepping t=0.3360635393397865, i=2097152
--- stepping t=0.3484735666418466, i=2097152
--- stepping t=0.3608835939439066, i=2097152
--- stepping t=0.3732936212459667, i=2097152
--- stepping t=0.38570364854802675, i=2097152
--- stepping t=0.39811367585008683, i=2097152
--- stepping t=0.41052370315214687, i=2097152
--- stepping t=0.42293373045420696, i=2097152
--- stepping t=0.43534375775626705, i=2097152
--- stepping t=0.4477537850583271, i=2097152
--- stepping t=0.46016381236038717, i=2097152
--- stepping t=0.4725738396624472, i=2097152
--- stepping t=0.4849838669645073, i=2097152
--- stepping t=0.4973938942665673, i=2097152
--- stepping t=0.5098039215686274, i=2097152
--- stepping t=0.5222139488706875, i=2097152
--- stepping t=0.5346239761727475, i=2097152
--- stepping t=0.5470340034748076, i=2097152
--- stepping t=0.5594440307768677, i=2097152
--- stepping t=0.5718540580789278, i=2097152
--- stepping t=0.5842640853809877, i=2097152
--- stepping t=0.5966741126830478, i=2097152
--- stepping t=0.6090841399851079, i=2097152
--- stepping t=0.621494167287168, i=2097152
--- stepping t=0.6339041945892281, i=2097152
--- stepping t=0.6463142218912881, i=2097152
--- stepping t=0.6587242491933482, i=2097152
--- stepping t=0.6711342764954082, i=2097152
--- stepping t=0.6835443037974683, i=2097152
--- stepping t=0.6959543310995283, i=2097152
--- stepping t=0.7083643584015884, i=2097152
--- stepping t=0.7207743857036485, i=2097152
--- stepping t=0.7331844130057086, i=2097152
--- stepping t=0.7455944403077686, i=2097152
--- stepping t=0.7580044676098286, i=2097152
--- stepping t=0.7704144949118887, i=2097152
--- stepping t=0.7828245222139488, i=2097152
--- stepping t=0.7952345495160088, i=2097152
--- stepping t=0.8076445768180689, i=2097152
--- stepping t=0.820054604120129, i=2097152
--- stepping t=0.8324646314221891, i=2097152
--- stepping t=0.8448746587242492, i=2097152
--- stepping t=0.8572846860263091, i=2097152
--- stepping t=0.8696947133283692, i=2097152
--- stepping t=0.8821047406304293, i=2097152
--- stepping t=0.8945147679324894, i=2097152
--- stepping t=0.9069247952345494, i=2097152
--- stepping t=0.9193348225366095, i=2097152
--- stepping t=0.9317448498386696, i=2097152
--- stepping t=0.9441548771407297, i=2097152
--- stepping t=0.9565649044427896, i=2097152
--- stepping t=0.9689749317448497, i=2097152
--- stepping t=0.9813849590469098, i=2097152
--- stepping t=0.9937949863489699, i=2097152
Running with 5 steps, ff=4...
--- stepping t=0.14215686274509803, i=2097152
--- stepping t=0.38725490196078427, i=2097152
--- stepping t=0.6323529411764706, i=2097152
--- stepping t=0.8774509803921569, i=2097152
Running with 10 steps, ff=4...
--- stepping t=0.07407407407407407, i=2097152
--- stepping t=0.1830065359477124, i=2097152
--- stepping t=0.29193899782135074, i=2097152
--- stepping t=0.40087145969498905, i=2097152
--- stepping t=0.5098039215686274, i=2097152
--- stepping t=0.6187363834422658, i=2097152
--- stepping t=0.7276688453159041, i=2097152
--- stepping t=0.8366013071895424, i=2097152
--- stepping t=0.9455337690631808, i=2097152
Running with 20 steps, ff=4...
--- stepping t=0.04540763673890609, i=2097152
--- stepping t=0.09700722394220845, i=2097152
--- stepping t=0.14860681114551083, i=2097152
--- stepping t=0.2002063983488132, i=2097152
--- stepping t=0.2518059855521156, i=2097152
--- stepping t=0.30340557275541796, i=2097152
--- stepping t=0.3550051599587203, i=2097152
--- stepping t=0.40660474716202266, i=2097152
--- stepping t=0.45820433436532504, i=2097152
--- stepping t=0.5098039215686274, i=2097152
--- stepping t=0.5614035087719298, i=2097152
--- stepping t=0.6130030959752322, i=2097152
--- stepping t=0.6646026831785345, i=2097152
--- stepping t=0.7162022703818369, i=2097152
--- stepping t=0.7678018575851393, i=2097152
--- stepping t=0.8194014447884417, i=2097152
--- stepping t=0.8710010319917441, i=2097152
--- stepping t=0.9226006191950464, i=2097152
--- stepping t=0.9742002063983487, i=2097152
Running with 40 steps, ff=4...
--- stepping t=0.03217697335344394, i=2097152
--- stepping t=0.05731523378582202, i=2097152
--- stepping t=0.0824534942182001, i=2097152
--- stepping t=0.10759175465057817, i=2097152
--- stepping t=0.13273001508295626, i=2097152
--- stepping t=0.15786827551533433, i=2097152
--- stepping t=0.1830065359477124, i=2097152
--- stepping t=0.20814479638009048, i=2097152
--- stepping t=0.23328305681246855, i=2097152
--- stepping t=0.2584213172448466, i=2097152
--- stepping t=0.28355957767722473, i=2097152
--- stepping t=0.3086978381096028, i=2097152
--- stepping t=0.3338360985419809, i=2097152
--- stepping t=0.3589743589743589, i=2097152
--- stepping t=0.384112619406737, i=2097152
--- stepping t=0.40925087983911507, i=2097152
--- stepping t=0.43438914027149317, i=2097152
--- stepping t=0.45952740070387127, i=2097152
--- stepping t=0.4846656611362493, i=2097152
--- stepping t=0.5098039215686274, i=2097152
--- stepping t=0.5349421820010055, i=2097152
--- stepping t=0.5600804424333835, i=2097152
--- stepping t=0.5852187028657616, i=2097152
--- stepping t=0.6103569632981397, i=2097152
--- stepping t=0.6354952237305178, i=2097152
--- stepping t=0.6606334841628959, i=2097152
--- stepping t=0.6857717445952739, i=2097152
--- stepping t=0.710910005027652, i=2097152
--- stepping t=0.7360482654600301, i=2097152
--- stepping t=0.7611865258924082, i=2097152
--- stepping t=0.7863247863247862, i=2097152
--- stepping t=0.8114630467571643, i=2097152
--- stepping t=0.8366013071895424, i=2097152
--- stepping t=0.8617395676219205, i=2097152
--- stepping t=0.8868778280542986, i=2097152
--- stepping t=0.9120160884866766, i=2097152
--- stepping t=0.9371543489190547, i=2097152
--- stepping t=0.9622926093514328, i=2097152
--- stepping t=0.9874308697838109, i=2097152
Running with 80 steps, ff=4...
--- stepping t=0.025812856788284932, i=2097152
--- stepping t=0.038222884090344994, i=2097152
--- stepping t=0.05063291139240506, i=2097152
--- stepping t=0.06304293869446512, i=2097152
--- stepping t=0.07545296599652519, i=2097152
--- stepping t=0.08786299329858525, i=2097152
--- stepping t=0.10027302060064532, i=2097152
--- stepping t=0.11268304790270538, i=2097152
--- stepping t=0.12509307520476545, i=2097152
--- stepping t=0.13750310250682551, i=2097152
--- stepping t=0.14991312980888558, i=2097152
--- stepping t=0.16232315711094564, i=2097152
--- stepping t=0.1747331844130057, i=2097152
--- stepping t=0.18714321171506576, i=2097152
--- stepping t=0.19955323901712582, i=2097152
--- stepping t=0.21196326631918588, i=2097152
--- stepping t=0.22437329362124595, i=2097152
--- stepping t=0.236783320923306, i=2097152
--- stepping t=0.24919334822536607, i=2097152
--- stepping t=0.26160337552742613, i=2097152
--- stepping t=0.2740134028294862, i=2097152
--- stepping t=0.28642343013154625, i=2097152
--- stepping t=0.29883345743360634, i=2097152
--- stepping t=0.3112434847356664, i=2097152
--- stepping t=0.32365351203772647, i=2097152
--- stepping t=0.3360635393397865, i=2097152
--- stepping t=0.3484735666418466, i=2097152
--- stepping t=0.3608835939439066, i=2097152
--- stepping t=0.3732936212459667, i=2097152
--- stepping t=0.38570364854802675, i=2097152
--- stepping t=0.39811367585008683, i=2097152
--- stepping t=0.41052370315214687, i=2097152
--- stepping t=0.42293373045420696, i=2097152
--- stepping t=0.43534375775626705, i=2097152
--- stepping t=0.4477537850583271, i=2097152
--- stepping t=0.46016381236038717, i=2097152
--- stepping t=0.4725738396624472, i=2097152
--- stepping t=0.4849838669645073, i=2097152
--- stepping t=0.4973938942665673, i=2097152
--- stepping t=0.5098039215686274, i=2097152
--- stepping t=0.5222139488706875, i=2097152
--- stepping t=0.5346239761727475, i=2097152
--- stepping t=0.5470340034748076, i=2097152
--- stepping t=0.5594440307768677, i=2097152
--- stepping t=0.5718540580789278, i=2097152
--- stepping t=0.5842640853809877, i=2097152
--- stepping t=0.5966741126830478, i=2097152
--- stepping t=0.6090841399851079, i=2097152
--- stepping t=0.621494167287168, i=2097152
--- stepping t=0.6339041945892281, i=2097152
--- stepping t=0.6463142218912881, i=2097152
--- stepping t=0.6587242491933482, i=2097152
--- stepping t=0.6711342764954082, i=2097152
--- stepping t=0.6835443037974683, i=2097152
--- stepping t=0.6959543310995283, i=2097152
--- stepping t=0.7083643584015884, i=2097152
--- stepping t=0.7207743857036485, i=2097152
--- stepping t=0.7331844130057086, i=2097152
--- stepping t=0.7455944403077686, i=2097152
--- stepping t=0.7580044676098286, i=2097152
--- stepping t=0.7704144949118887, i=2097152
--- stepping t=0.7828245222139488, i=2097152
--- stepping t=0.7952345495160088, i=2097152
--- stepping t=0.8076445768180689, i=2097152
--- stepping t=0.820054604120129, i=2097152
--- stepping t=0.8324646314221891, i=2097152
--- stepping t=0.8448746587242492, i=2097152
--- stepping t=0.8572846860263091, i=2097152
--- stepping t=0.8696947133283692, i=2097152
--- stepping t=0.8821047406304293, i=2097152
--- stepping t=0.8945147679324894, i=2097152
--- stepping t=0.9069247952345494, i=2097152
--- stepping t=0.9193348225366095, i=2097152
--- stepping t=0.9317448498386696, i=2097152
--- stepping t=0.9441548771407297, i=2097152
--- stepping t=0.9565649044427896, i=2097152
--- stepping t=0.9689749317448497, i=2097152
--- stepping t=0.9813849590469098, i=2097152
--- stepping t=0.9937949863489699, i=2097152