Motivation
Unlocking the full potential of next-generation cosmological data requires navigating the balance between sophisticated physics models and computational demands. We propose a solution by introducing a machine learning-based field-level emulator within the HMC-based Bayesian Origin Reconstruction from Galaxies (BORG) inference algorithm. The emulator, an extension of the first-order Lagrangian Perturbation Theory (LPT), achieves remarkable accuracy compared to $N$-body simulations while significantly reducing evaluation time. Leveraging its differentiable neural network architecture, the emulator enables efficient sampling of the high-dimensional space of cosmic initial conditions. To demonstrate its efficacy, we use the inferred posterior samples of initial conditions to run posterior resimulations with $N$-body simulations, yielding highly accurate present-day non-linear dark matter fields compared to the underlying truth used during inference.
Field-Level Emulator
In this work, we build upon the work of Jamieson et al (2022) by incorporating the convolutional neural network (CNN) emulator into the physical forward model of BORG. While an $N$-body simulation aims to translate initial particle positions into their final positions, which represent the non-linear dark matter distribution, several approximate models strive for the same result with a lower computational cost. Specifically, our emulator aims to use as input first-order LPT and correct it such that the output of the emulator aligns with the results of an actual $N$-body simulation. The emulator effectively bridges the gap between $1$LPT and $N$-body outcomes; while the $1$LPT struggles to replicate collapsed overdensities as effectively as the $N$-body simulation, the emulator achieves remarkable success in reproducing $N$-body-like cosmic structures.
 Visual comparison of three physical forward models at redshift $z=0$, illustrated in the panels as slices through the density field. $128^3$ particles in a cubic volume with side length $250h^{-1}$ Mpc were simulated. Identical initial conditions underpin the $N$-body simulation, the first-order Lagrangian Perturbation Theory ($1$LPT), and the emulator (BORG-EM). In the right-most panel, the $N$-body simulation’s initial conditions originate from the posterior distribution realized through the BORG algorithm. The inference process employs the $N$-body density field (the left-most panel) combined with Gaussian noise as the ground truth, utilizing the BORG-EM as the forward model during inference. As expected, given that this represents a single realization of posterior resimulations of initial conditions, minor deviations from the true $N$-body field are visible. Being able to capture large-scale structures as well as collapsed overdensities, the field-level emulator demonstrates that field-level inference from non-linear cosmic structures is feasible.
Visual comparison of three physical forward models at redshift $z=0$, illustrated in the panels as slices through the density field. $128^3$ particles in a cubic volume with side length $250h^{-1}$ Mpc were simulated. Identical initial conditions underpin the $N$-body simulation, the first-order Lagrangian Perturbation Theory ($1$LPT), and the emulator (BORG-EM). In the right-most panel, the $N$-body simulation’s initial conditions originate from the posterior distribution realized through the BORG algorithm. The inference process employs the $N$-body density field (the left-most panel) combined with Gaussian noise as the ground truth, utilizing the BORG-EM as the forward model during inference. As expected, given that this represents a single realization of posterior resimulations of initial conditions, minor deviations from the true $N$-body field are visible. Being able to capture large-scale structures as well as collapsed overdensities, the field-level emulator demonstrates that field-level inference from non-linear cosmic structures is feasible.
BORG-EM
BORG (Bayesian Origin Reconstruction from Galaxies) obtains data-constrained realizations of a set of plausible three-dimensional initial conditions in the form of the white noise amplitudes $\mathbf{x}$ given some data $\mathbf{d}$, such as a dark matter over-density field or an observed galaxy counts. A schematic of the incorporation of the field-level emulator into BORG, which we call BORG-EM, is shown in the figure below. The initial white-noise field $\mathbf{x}$ is evolved using BORG-1LPT to redshift $z=0$. We obtain the $3$-dimensional displacements $\Psi_{\mathrm{LPT}}$ using the $1$LPT predicted particle positions $p_{\mathrm{LPT}}$ and the initial grid positions $q$. The displacements are corrected through the use of the emulator, yielding the updated displacements $\Psi_{\mathrm{EM}}$ and, in turn, the particle positions. The Cloud-In-Cell (CIC) algorithm is applied as the particle mesh assignment scheme, which gives us the effective number of particles per voxel and, subsequently, the final overdensity field $\boldsymbol{\delta}$ at $z=0$. After a likelihood computation, the adjoint gradient is back-propagated through the combined structure formation model (BORG-EM) to the initial white-noise field $\mathbf{x}$.
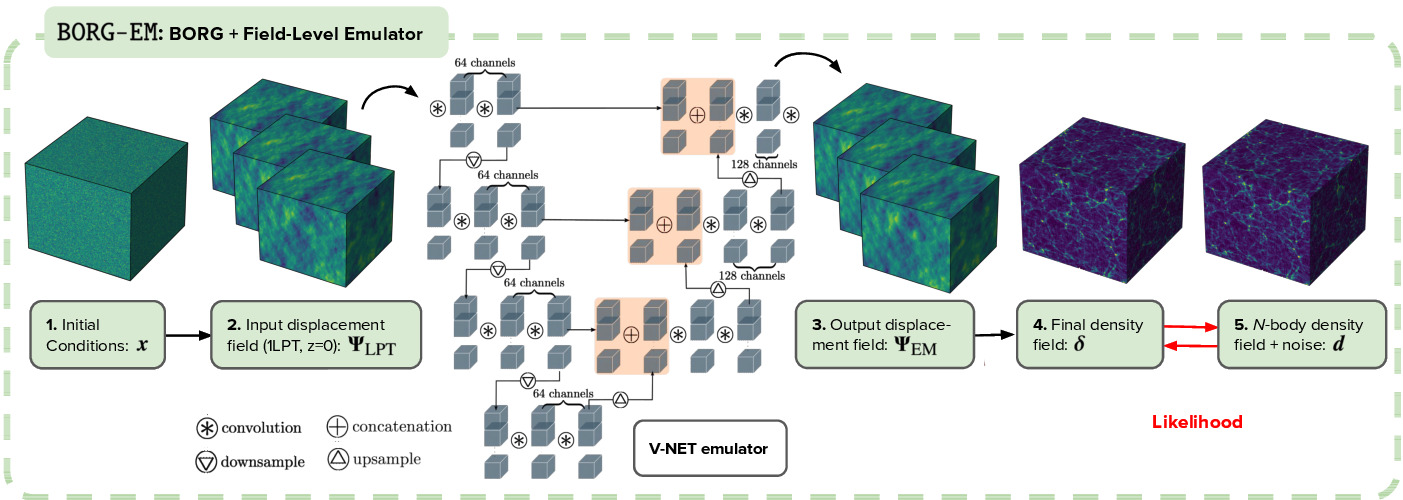 Overview of the field-level emulator integration within the BORG algorithm, which we call BORG-EM.
Overview of the field-level emulator integration within the BORG algorithm, which we call BORG-EM.
Posterior Resimulations
A sufficiently accurate physics model is needed during inference to recover the initial conditions accurately (S. Stopyra et al. 2023). To validate the incorporation of the emulator in field-level inference, we use $80$ independent posterior samples of inferred initial conditions within the $N$-body simulator P-Gadget-III, mirroring the data generation setup. The posterior resimulations align with the ground truth $N$-body simulation in the formation of massive large-scale structures, in terms of halo mass function as well as density profiles, which demonstrates the robustness of the emulator model in inference. We display the average over the stacked density profiles as well as the standard error in the figure below.
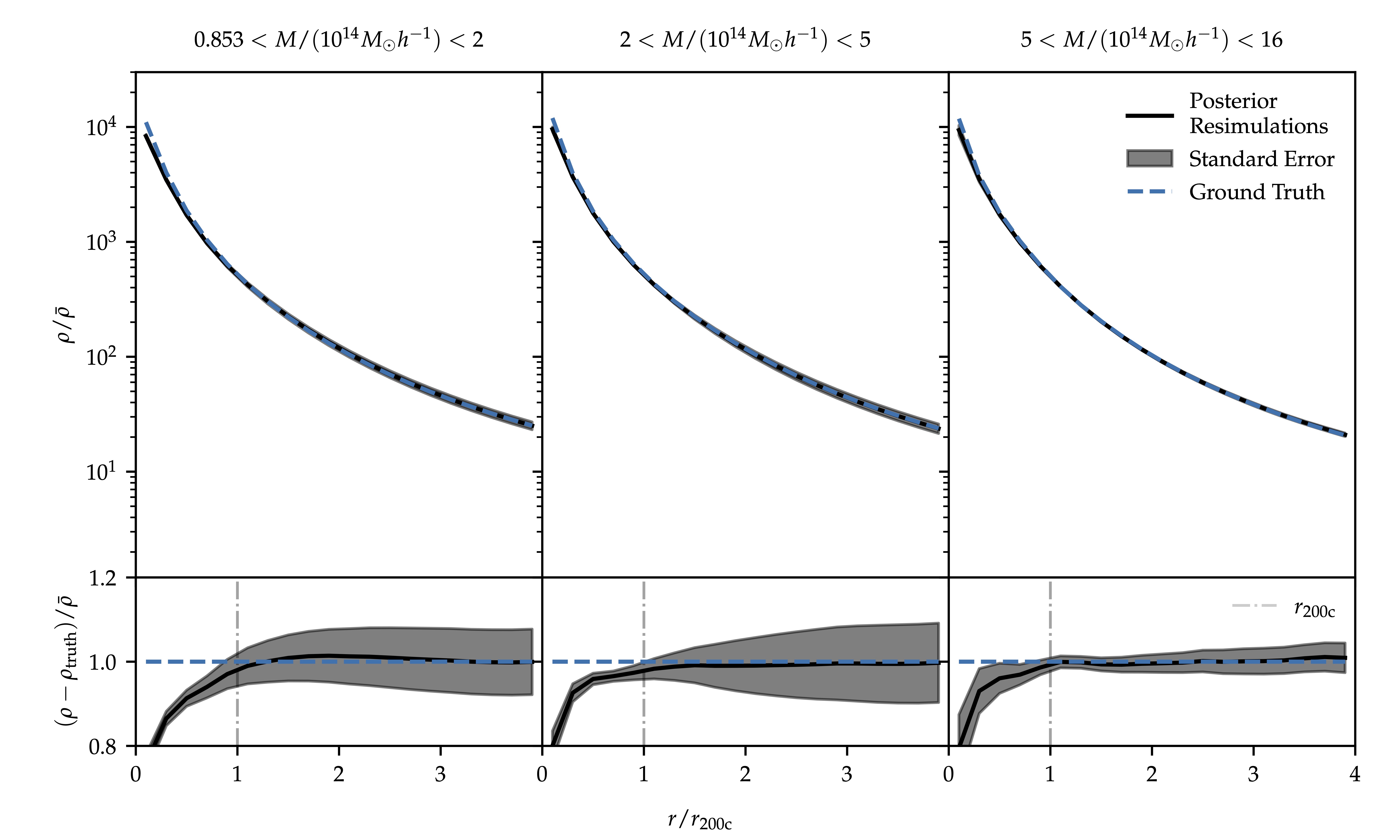 Stacked halo density profiles obtained from the posterior resimulations and the ground truth in three distinct mass bins. For all mass bins, as compared to the ground truth, we see at most a $10\%$ discrepancy down to $\frac{1}{2}r_{200\mathrm{c}}$, highlighting the high quality of the sampled initial conditions by BORG-EM. It is worth noting that the virial radius $r_{200\mathrm{c}}$ for the ground truth haloes lie in the range $[0.34,1.85]h^{-1}$ Mpc, i.e. below the data resolution ($1.95h^{-1}$ Mpc).
Stacked halo density profiles obtained from the posterior resimulations and the ground truth in three distinct mass bins. For all mass bins, as compared to the ground truth, we see at most a $10\%$ discrepancy down to $\frac{1}{2}r_{200\mathrm{c}}$, highlighting the high quality of the sampled initial conditions by BORG-EM. It is worth noting that the virial radius $r_{200\mathrm{c}}$ for the ground truth haloes lie in the range $[0.34,1.85]h^{-1}$ Mpc, i.e. below the data resolution ($1.95h^{-1}$ Mpc).
Future work
In this work, we tested the incorporation of the field-level emulators in BORG for sampling cosmic initial conditions using mock data based on non-linear large-scale structures from $N$-body simulations and Gaussian noise. Posterior resimulations – using the inferred initial conditions for $N$-body simulations – show that the recovery of information in the initial conditions is sufficient to accurately reproduce halo properties. In particular, we show highly accurate $M_{200\mathrm{c}}$ halo mass function and stacked density profiles of haloes in different mass bins $[0.853,16]\times 10^{14}M_{\odot}h^{-1}$. As all available cross-correlation information is extracted, we acknowledge that limitations in recovering the initial conditions stem from the noise level and data grid resolution. This is promising as it underscores the significance of accurate non-linear modeling, indicating the potential for extracting additional information at smaller scales.
References
- Ludvig Doeser, Drew Jamieson, Stephen Stopyra, Guilhem Lavaux, Florent Leclercq, Jens Jasche, 2023, submitted to MNRAS, arXiv:2312.09271
- Drew Jamieson, Yin Li, Renan Alves de Oliveira, Francisco Villaescusa-Navarro, Shirley Ho, David N. Spergel, 2022, arXiv:2206.04594
- Stephen Stopyra, Hiranya V. Peiris, Andrew Pontzen, Jens Jasche, Guilhem Lavaux, 2023, submitted to MNRAS, arXiv:2304.09193