Overview
There are about two trillion galaxies in the observable Universe, and the evolution of each of them is sensitive to the presence of all the others. Can we put this all into a computer, or even a mobile phone, to simulate the evolution of the Universe? In a recent paper, we introduced a perfectly parallel algorithm for cosmological simulations which addresses this question.
Modern cosmology relies on very large data sets to determine the content of our Universe, in particular the amounts of dark matter and dark energy. These large datasets include the positions and electromagnetic spectra of very distant galaxies, up to 20 billion light-years away. In the next decade, the Euclid mission1 and the Vera Rubin observatory,2 in particular, will obtain information on several billion galaxies.
Physical challenges
Making the link between our knowledge of physics, for example the equations that govern the evolution of dark matter and dark energy, and astronomical observations requires considerable computational resources. Indeed, the most recent observations cover huge volumes: of the order of that of a cube of 12 billion light-years side length. As the typical distance between two galaxies is only a few million light-years, we have to simulate around one trillion galaxies to reproduce the observations.
In addition, in order to follow the physics of the formation of these galaxies, the spatial resolution should be of the order of ten light-years. Ideally, simulations should therefore have a scale ratio (that is, the ratio between the largest and smallest physical lengths of the problem) close to a billion. No computer, existing or even under construction, can achieve such a goal.
In practice, it is therefore necessary to use approximate techniques, consisting in “populating” the large-scale structures of the Universe with fictitious (but realistic) galaxies. This approximation is further justified by the fact that the evolution of galaxies’ components, for example stars and interstellar gas, involves very fast phenomena in comparison to the global evolution of the cosmos. The use of fictitious galaxies still requires simulating the dynamics of the Universe with a scale ratio of around 4,000, which is just possible with today’s supercomputers.
The problem of computational limits
Simulating the gravitational dynamics of the Universe is what physicists call a \(N\)-body problem. Although the equations to be solved are analytical, as in most cases in physics, solutions have no simple expressions and require numerical techniques as soon as \(N\) is larger than four. The direct numerical solution consists in explicitly calculating the interactions between all the pairs of bodies, also called “particles”. The computation of forces by direct summation was the favoured technique in cosmology at the beginning of the development of numerical simulations, in the 1970s. At present, it is mainly used for simulations of star clusters and galactic centres. The number of particles used in “direct summation” simulations is represented by green dots in figure 1, where the \(y\)-axis has a logarithmic scale.
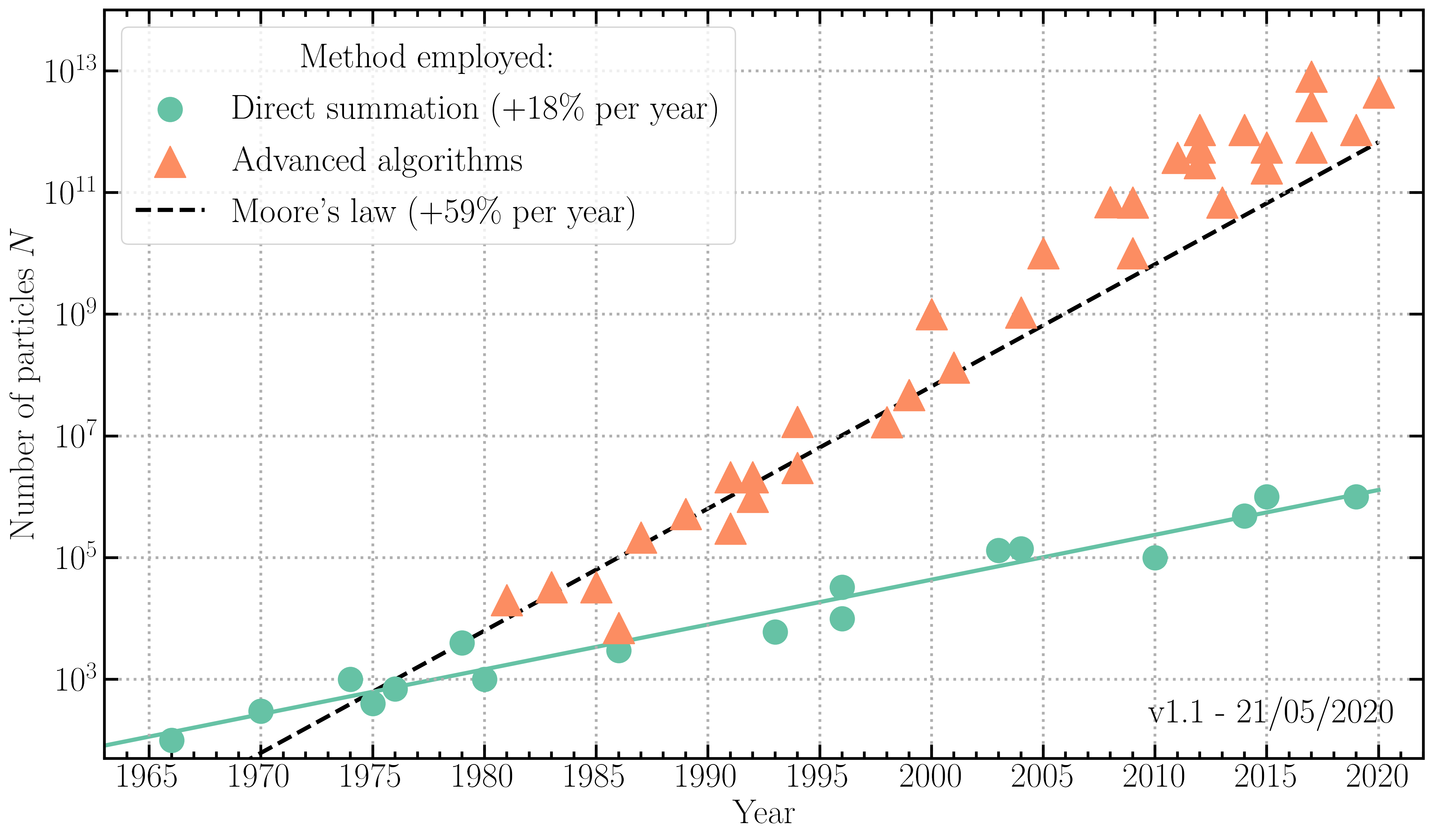 Evolution of the number of particles used in \(N\)-body simulations as a function of year of publication. Different symbols and colours correspond to different methods used to compute gravitational dynamics (direct summation in green, advanced algorithms in orange). For comparison, Moore’s law concerning computer performance is represented by the black dotted line.
Evolution of the number of particles used in \(N\)-body simulations as a function of year of publication. Different symbols and colours correspond to different methods used to compute gravitational dynamics (direct summation in green, advanced algorithms in orange). For comparison, Moore’s law concerning computer performance is represented by the black dotted line.
The direct summation method has a numerical cost which increases like \(N^2\), the number of pairs of particles considered. For this reason, in spite of improvements provided by hardware accelerators such as graphics processing unit (GPUs), the number of particles used with this method cannot grow as quickly as in the famous “Moore’s Law”, which predicts a doubling of computer hardware performance every 18 months. Moore’s law was verified for about four decades (1965-2005), but as traditional hardware architectures are reaching their physical limit, the performance of individual compute cores attained a plateau around 2015 (see figure 2). Therefore, cosmological simulations cannot merely rely on processors becoming faster to reduce the computational time.
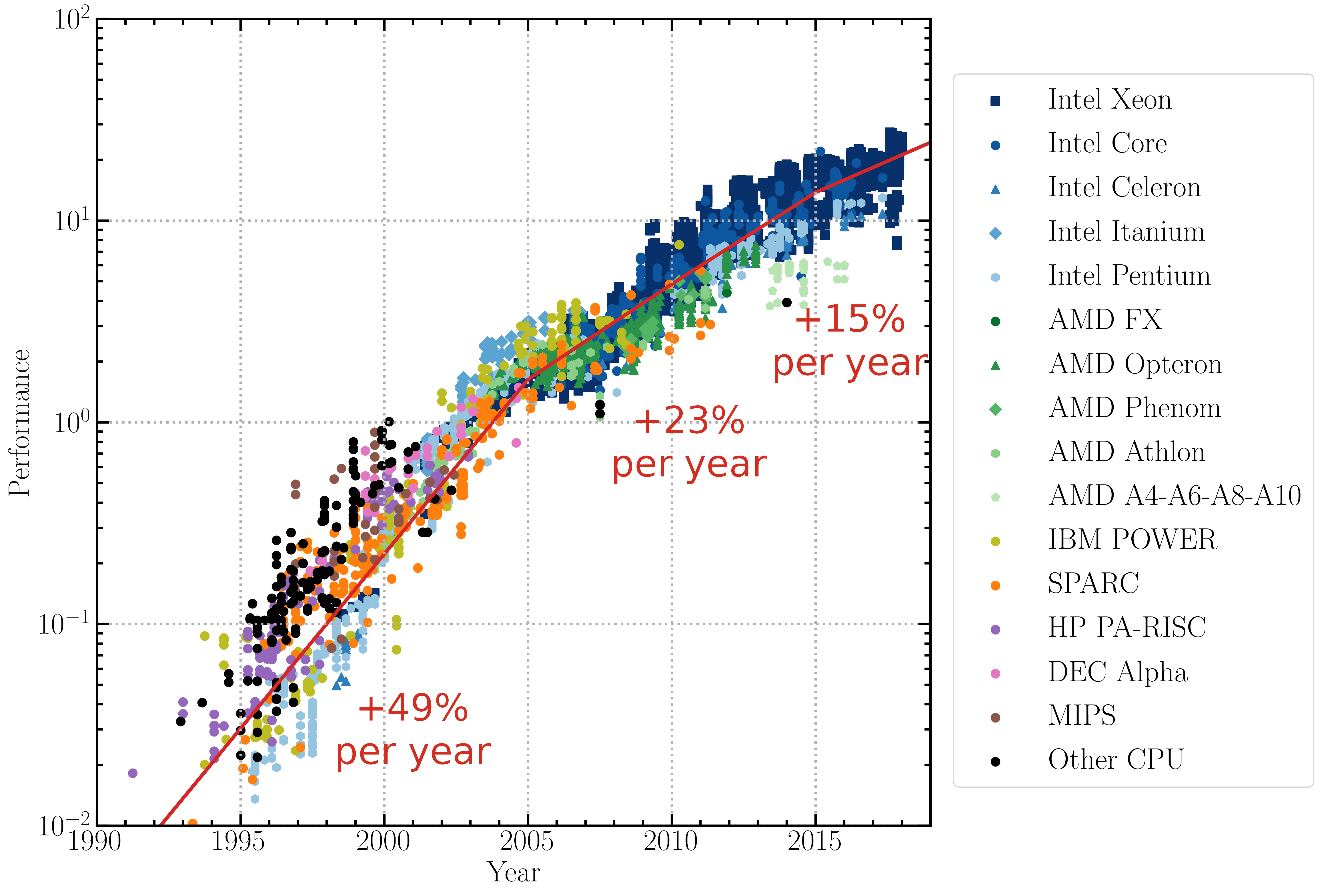 Single-threaded floating point performance of CPUs as a function of time. Different trademarks and models are represented by different colours and symbols as indicated in the caption. This plot is based on adjusted SPECfp® results.3
Single-threaded floating point performance of CPUs as a function of time. Different trademarks and models are represented by different colours and symbols as indicated in the caption. This plot is based on adjusted SPECfp® results.3
In order to reduce the cost of simulations, most of the work in numerical cosmology since 1980 has consisted in improving algorithms. The aim was to circumvent the explicit calculation of all gravitational interactions between particles, especially for pairs which are the most distant in the volume to be simulated. These algorithmic developments have enabled a huge increase in the number of particles used in cosmological simulations (see the orange triangles in figure 1). In fact, since 1990, the increase in computational capacity in cosmology has been faster than Moore’s Law, with software improvements adding to the increase in computer performance (more details in this blog post).
In 2020, with the architectures of modern supercomputers, calculations are no longer limited by the number of operations that processors can perform in a given time, but by the inherent latencies in communications among the different processors involved in so-called “parallel” calculations. In these computational techniques, a large number of processors work together synchronously to perform calculations far too complex to be carried out on a conventional computer. The stagnation of performances due communication latencies has been theorised in “Amdahl’s law” (see figure 3), named after the computer scientist who formulated it in 1967. It is now the main challenge for cosmological simulations: without improving the “degree of parallelism” of our algorithms, we will soon reach a technological plateau.
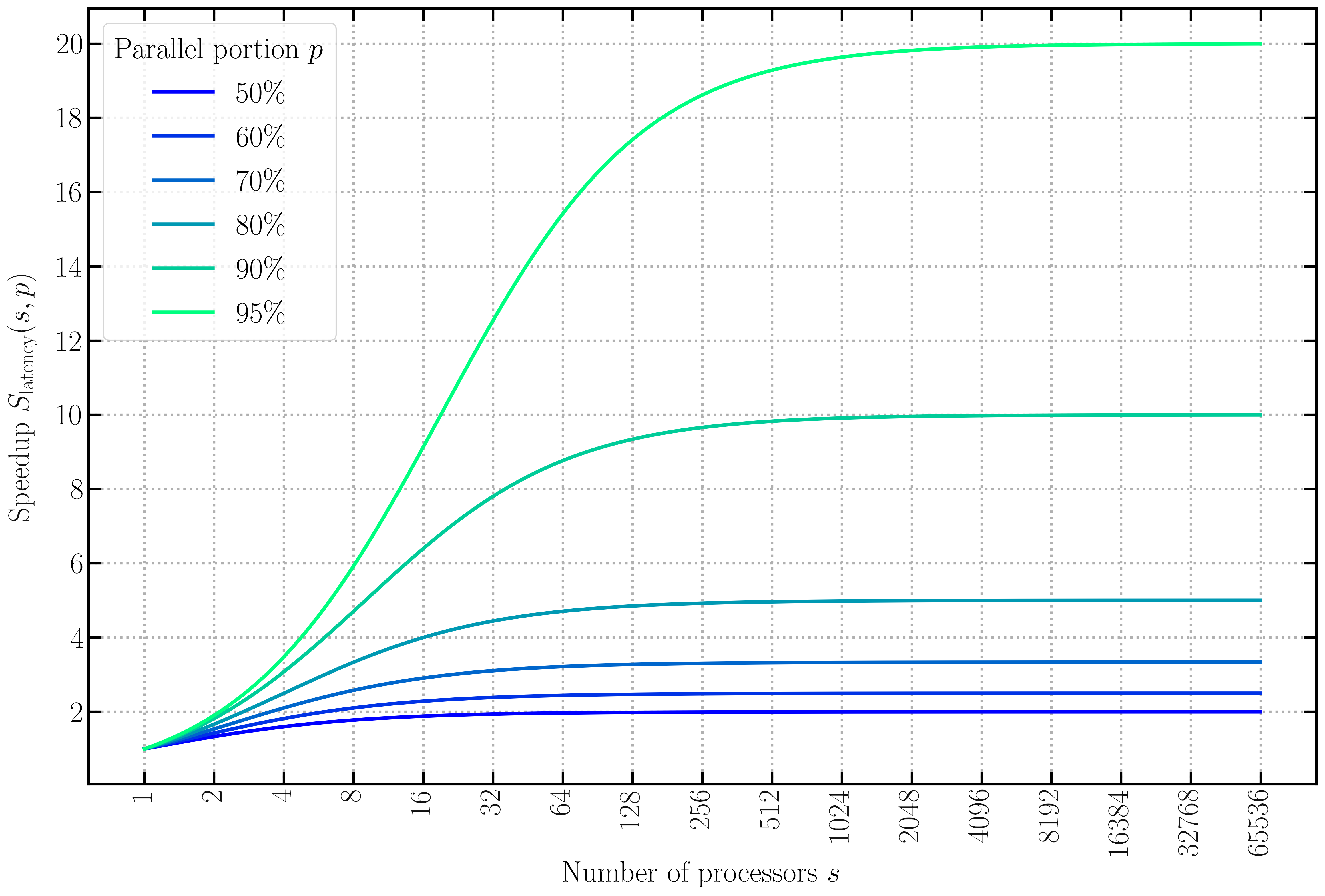 Amdahl’s law: theoretical speed-up in the execution of a program as a function of the number of processors executing it, for different values of the parallel fraction of the program (different lines). The speed-up is limited by the serial part of the program. For example, if 90% of the program can be parallelised, the theoretical maximum speed-up factor using a large number of processors would be 10.
Amdahl’s law: theoretical speed-up in the execution of a program as a function of the number of processors executing it, for different values of the parallel fraction of the program (different lines). The speed-up is limited by the serial part of the program. For example, if 90% of the program can be parallelised, the theoretical maximum speed-up factor using a large number of processors would be 10.
The sCOLA approach: divide and conquer
Let us go back to the physical problem to be solved: it is about simulating the gravitational dynamics of the Universe at different scales. At “small” scales, there are many objects that interact with each other: numerical simulations are required. But at “large” spatial scales, that is to say if we look at figure 4 from very far, not much happens during evolution (except for a linear increase of the amplitude of inhomogeneities). Despite this, with traditional simulation algorithms, the gravitational effect of all the particles on each other must be calculated, even if they are very far apart. It is expensive and almost useless, since most of gravitational evolution is correctly described by simple equations, which can be solved analytically without a computer.
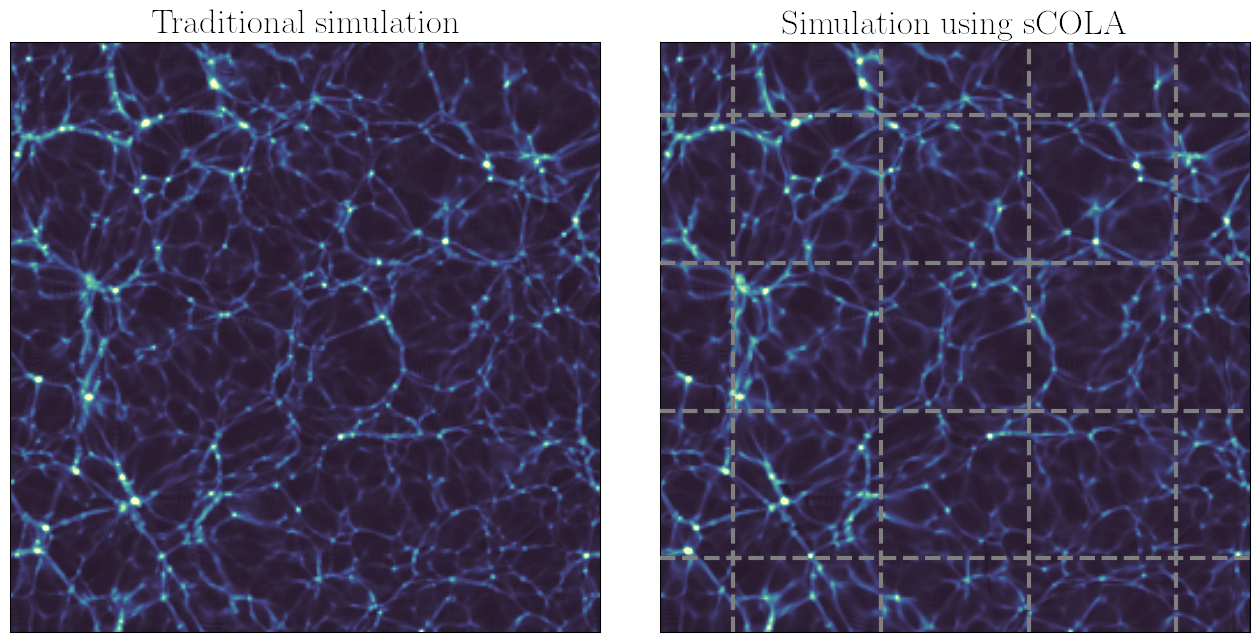 Comparison between a traditional simulation (left panel) and a simulation using our new algorithm (right panel). In our approach, the volume of the simulation is a mosaic made of “tiles” calculated independently and whose edges are represented by dotted lines.
Comparison between a traditional simulation (left panel) and a simulation using our new algorithm (right panel). In our approach, the volume of the simulation is a mosaic made of “tiles” calculated independently and whose edges are represented by dotted lines.
In order to minimise unnecessary numerical calculations, it is possible to use a hybrid simulation algorithm: analytical at large scales and numerical at small scales. The underlying idea, called spatial comoving Lagrangian acceleration (sCOLA4), is common in physics: it is a “change of frame of reference”. In this framework, large-scale dynamics is taken into account by the new frame of reference, while small-scale dynamics is solved numerically by the computer, using conventional calculations of the gravity field. Unfortunately, the most naive version of the sCOLA algorithm gives results that are too approximate to be usable. In our last publication,5 we modified sCOLA in order to improve its accuracy.
Furthermore, we have realised that this concept makes it possible to “divide and conquer”. Indeed, given a large volume to be simulated, sCOLA allows sub-volumes of smaller size to be simulated independently, without communication with neighbouring sub-volumes. Our approach therefore makes it possible to represent the Universe as a large mosaic: each of the “tiles” in figure 4 is a small simulation that a modest computer can solve, and the assembly of all the tiles gives the overall picture. This is what is called in computer science a “perfectly parallel” algorithm, unlike all cosmological simulation algorithms so far. Thanks to it, we have been able to obtain cosmological simulations at a satisfactory resolution, while remaining on a relatively modest computing facility (figure 5).
Our perfectly parallel sCOLA algorithm has been implemented in the publicly available Simbelmynë code,6 where it is included in version 0.4.0 and later.
 A GPU-based computer at the Institut d’Astrophysique de Paris. Its costs represents only a hundredth of that of a supercomputer at national computing facilities.
A GPU-based computer at the Institut d’Astrophysique de Paris. Its costs represents only a hundredth of that of a supercomputer at national computing facilities.
New hardware to simulate the Universe
This new algorithm is not limited to being used in small computing facilities, but allows to envisage new ways of exploiting computing hardware. Ideally, each of the “tiles” could be small enough to fit in the “cache memory” of our computers, that is, the part of the memory that processors can access in the smallest amount of time. The resultant communication speed up would allow us to simulate the entire volume of the Universe extremely quickly, or even at a resolution never achieved so far.
Going further, we can even imagine that each of the simulations corresponding to a “tile” would be small enough that it can be run on a modern mobile phone! This parallelisation technique would be based on a platform such as Cosmology@Home7, which is dedicated to distributed collaborative computing. This platform is derived from the efforts initiated by SETI@Home8 for the search for extraterrestrial intelligence.
-
S. Tassev, D. J. Eisenstein, B. D. Wandelt, M. Zaldarriaga, sCOLA: The N-body COLA Method Extended to the Spatial Domain (2015), arXiv:1502.07751 ↩
-
F. Leclercq, B. Faure, G. Lavaux, B. D. Wandelt, A. H. Jaffe, A. F. Heavens, W. J. Percival, C. Noûs, Perfectly parallel cosmological simulations using spatial comoving Lagrangian acceleration, A&A, in press (2020), arXiv:2003.04925 ↩
Authored by F. Leclercq, G. Lavaux
Post identifier: /method/scola