Overview
Testing General Relativity on large scales is largely tantamount to searching for new fundamental interactions (‘‘fifth forces’’) between masses, mediated by dynamical fields beyond the metric tensor. An important competitor to General Relativity is galileon gravity, which introduces a new light scalar field with a Lagrangian that is symmetric under Galilean transformations. Historically the galileon has been a leading contender for explaining dark energy, but now it is viewed mainly as an archetype of ‘‘Vainshtein-screened’’ theories where the fifth force from the scalar field vanishes in high-density regions due to second derivative terms in the equation of motion. This behaviour arises in many theories beyond the Standard Model.
A key feature of the galileon is that it couples to nonrelativistic matter but not to gravitational binding energy, violating the strong equivalence principle. This means that black holes – the only purely gravitational objects – are entirely unaffected by the galileon, while the stars, gas and dark matter in galaxies feel the full fifth force. As illustrated in Figure 1, this causes the supermassive black holes at the centres of galaxies to lag behind the other galactic components in the direction of an external galileon field. We have used this effect in a recent article to place stringent constraints on the strength of a galileon coupling to matter.1
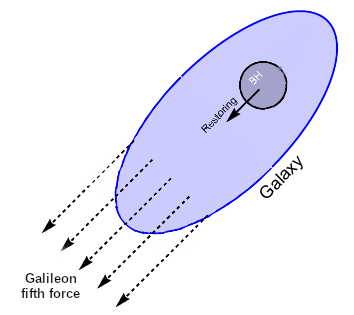 Cartoon illustrating the formation of galaxy–black hole offsets under galileon gravity. The restoring force on the black hole due to its offset from the galaxy centre compensates for the fact that it doesn’t feel the galileon fifth force.
Cartoon illustrating the formation of galaxy–black hole offsets under galileon gravity. The restoring force on the black hole due to its offset from the galaxy centre compensates for the fact that it doesn’t feel the galileon fifth force.
CSiBORG: Mapping the large-scale gravitational field
To make predictions for black hole positions in galileon gravity, we need to know the fifth-force field on a galaxy-by-galaxy basis. To do this we introduced CSiBORG (Constrained Simulations in BORG), a suite of ~100 RAMSES N-body simulations using initial conditions sampled from the posterior of the BORG-PM algorithm. CSiBORG gives an accurate picture of dark matter structures within \(\sim 250\) Mpc of the Milky Way with a mass resolution of \(4.4 \times 10^9 \text{M}_\odot\), including full propagation of the uncertainties in the initial conditions.
We use CSiBORG to map out the local galileon field in the linear, quasistatic approximation. Combined with a flexible model for halo structure, this allows us to calculate the expected galaxy–black hole offsets as a function of the galileon coupling coefficient and the radius within which the fifth force is suppressed by the Vainshtein mechanism, \(r_V\). We apply this to \(\sim 2000\) galaxies in which the offset has been measured by comparing optical images of galaxies to multi-wavelength observations of Active Galactic Nuclei. Marginalising over an empirical model describing astrophysical noise, we then use a Bayesian likelihood framework and MCMC algorithm to constrain the galileon parameters.
Constraining cosmological galileons
We find no evidence that black holes are offset from the centres of their hosts in the direction or with the relative magnitude expected from galileons. This allows us to place strong constraints on the strength of the galileon fifth force relative to gravity, \(\Delta G/G_N\). In the left panel of Figure 2 we show this constraint for four observational datasets as a function of \(r_V\): our final bound, driven by the largest sample, is \(\Delta G/G_N < 0.16\) at \(1\sigma\) confindence for \(r_V \lesssim \text{Gpc}\). In the right panel we translate this result to a constraint on the coupling coefficient \(\alpha\) as a function of the lengthscale that appears in the galileon action, known as the crossover scale \(r_c\). Figure 2 also shows previous constraints from Lunar Laser Ranging and the black hole in M87 as well as the expected relation between \(\alpha\) and \(r_c\) in a higher-dimensional modified gravity model that introduces galileons called DGP.
Enabled by BORG, ours is the first work to model a large-scale galileon field point-by-point in space. It is therefore the first to probe crossover scales as large as the observable universe, and the first to achieve statistically rigorous constraints. By supplementing our model with numerical solutions of the galileon equation of motion in the nonlinear regime it will be possible to push our bound to smaller \(r_c\), superseding the Lunar Laser Ranging result and ruling out the self-accelerating branch of DGP. More generally, a Monte Carlo-based forward-modelling approach calibrated against simulations and marginalised over noise holds great promise for precision tests of fundamental physics with galaxy survey datasets.
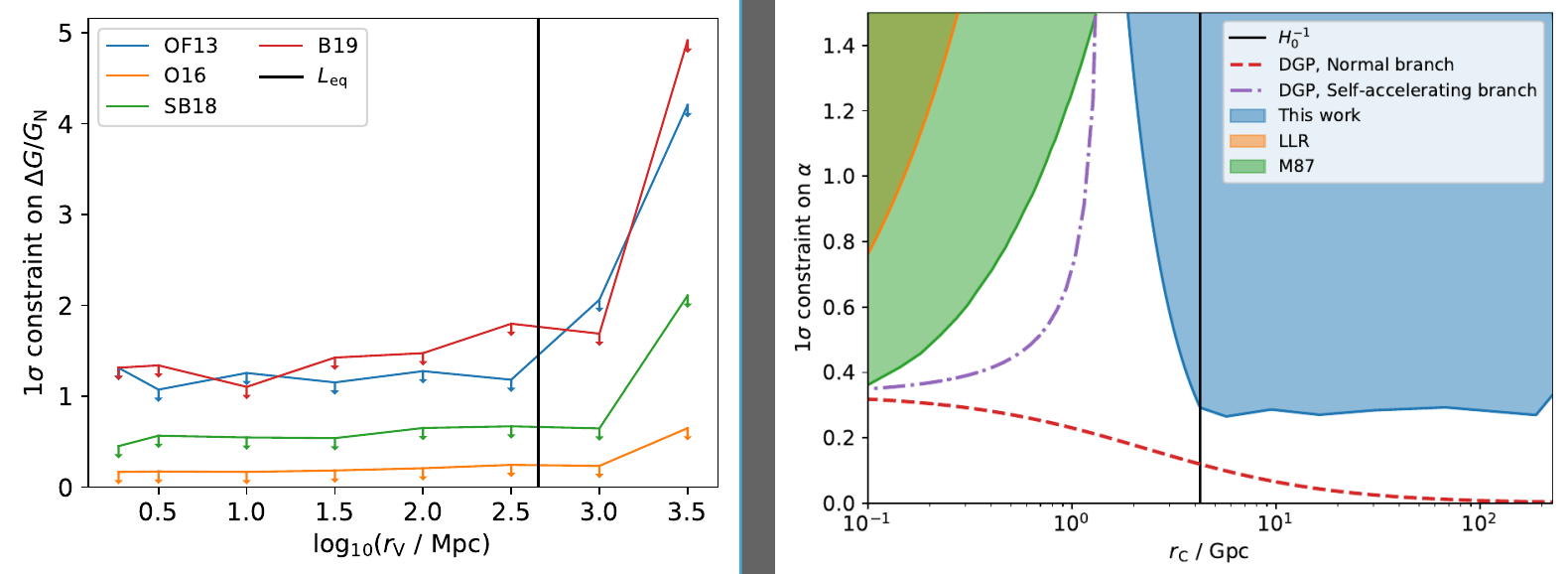 Left: \(1\sigma\) constraint on \(\Delta G/G_N\) as a function of average Vainshtein radius, \(rV\), from four observational datasets. \(L_{eq}\) is the length scale at which the matter power spectrum turns over. Right: Constraint on the coupling of a cubic galileon to matter, \(\alpha\), as a function of the crossover scale, \(r_c\), from lunar laser ranging (LLR), the black hole at the centre of M87, and our work. Our test probes larger-\(r_c\) galileons than others because it models the full galileon field from large-scale structure.
Left: \(1\sigma\) constraint on \(\Delta G/G_N\) as a function of average Vainshtein radius, \(rV\), from four observational datasets. \(L_{eq}\) is the length scale at which the matter power spectrum turns over. Right: Constraint on the coupling of a cubic galileon to matter, \(\alpha\), as a function of the crossover scale, \(r_c\), from lunar laser ranging (LLR), the black hole at the centre of M87, and our work. Our test probes larger-\(r_c\) galileons than others because it models the full galileon field from large-scale structure.
-
D. J. Bartlett, H. Desmond & P. G. Ferreira, 2020, ``Constraints on galileons from the positions of supermassive black holes’’, Phys Rev D submitted, arxiv 2010.05811
 ↩
↩
Authored by H. Desmond
Post identifier: /method/observations/bh_gravity