Overview of the problem

Accurate analyses of present and next-generation cosmological galaxy surveys require new ways to handle effects of non-linear gravitational structure formation processes in data. To address these needs we present an extension of our previously developed algorithm for Bayesian Origin Reconstruction from Galaxies to analyse matter clustering at non-linear scales in observations. This is achieved by incorporating a numerical particle mesh model of gravitational structure formation into our Bayesian inference framework.

A new technology

The algorithm simultaneously infers the three-dimensional primordial matter fluctuations from which present non-linear observations formed and provides reconstructions of velocity fields and structure formation histories. The physical forward modeling approach automatically accounts for the non-Gaussian features in gravitationally evolved matter density fields and addresses the redshift space distortion problem associated with peculiar motions of observed galaxies. Our algorithm employs a hierarchical Bayes approach to jointly account for various observational effects, such as unknown galaxy biases, selection effects, and observational noise. Corresponding parameters of the data model are marginalized out via a sophisticated Markov Chain Monte Carlo approach relying on a combination of a multiple block sampling framework and an efficient implementation of a Hamiltonian Monte Carlo sampler. We demonstrate the performance of the method by applying it to the 2M++ galaxy compilation, tracing the matter distribution of the Nearby Universe. We show accurate and detailed inferences of the three-dimensional non-linear dark matter distribution of the Nearby Universe. As exemplified in the case of the Coma cluster, our method provides complementary mass estimates that are compatible with those obtained from weak lensing and X-ray observations. For the first time, we also present a reconstruction of the vorticity of the non-linear velocity field from observations. In summary, our method provides plausible and very detailed inferences of the dark matter and velocity fields of our cosmic neighbourhood.

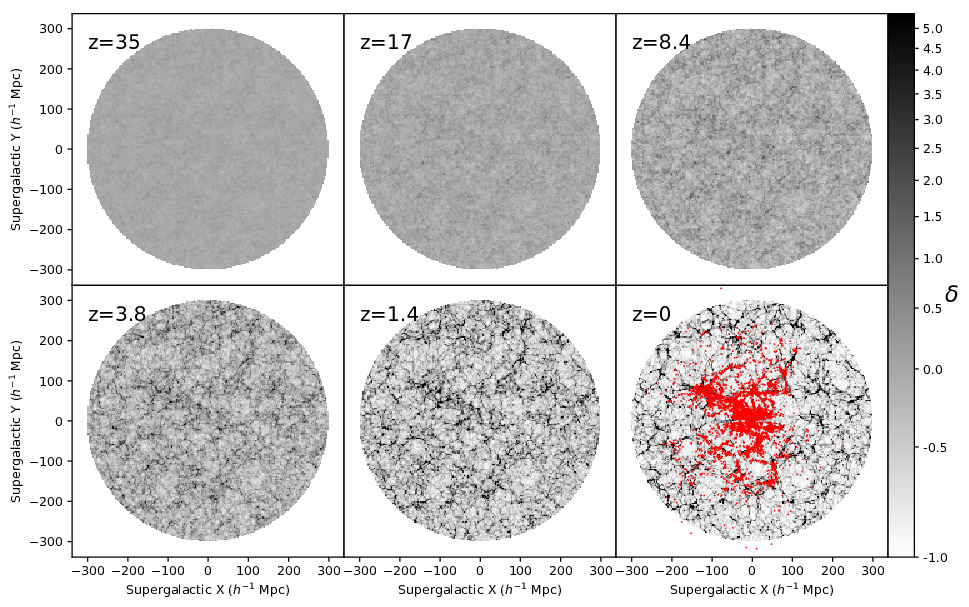This picture illustrates the capability to infer one plausible history of the formation of Large scale structures. The history reads from left to right, top to bottom. The ultimate snapshot shows the galaxies overlaying the inferred density field.

Applications in cosmology

Our method has applications in all fields in cosmology, either for direct measurements of underlying physical parameters or for comparing and correlating with other observations of same part of the Universe. In that work, we have only focused on three aspects: the measurement of masses of clusters and superclusters of galaxies, the properties of the peculiar velocity field on large scales and the study of claimed anomalies in the density fluctuations.

Cluster mass measurements

The first direct application is the measurement of the mass of clusters of galaxies. We have defined this mass in the simplest possible fashion: the total mass enclosed within a radius $r$, or mathematically speaking: \(M(r) = 4\pi\int_0^{R_\mathrm{max}} r^2 \rho(r)~\mathrm{d}r\,.\) We use for reference the mass enclosed if the the Universe content was strictly homogeneously distributed, or mathematically: \(M_\mathrm{mean}(r) = \frac{4\pi}{3} \rho_\mathrm{mean} r^3\,.\)

We showcase our estimator by focusing on one well studied object: the Coma cluster. The performance of our estimator is given in the Figure below. We clearly observe the compatibility of the measurement provided (solid lines and filled regions) through BORG-PM inference with the other probes considered in that study.

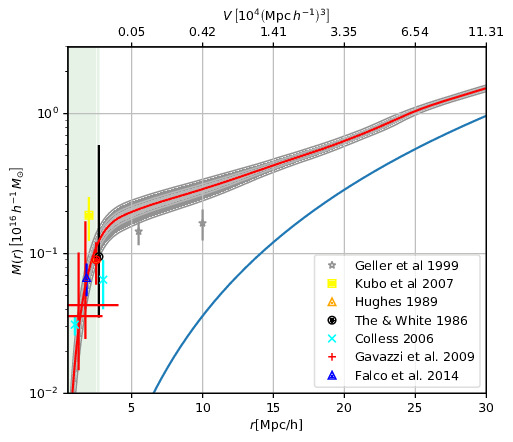The above pictures shows the mass profile, i.e. the mass enclosed within a given distance of the object, derived through different methods and data of the same cluster of galaxies: Coma. The BORG-PM method is given by the solid red line (mean mass profile), and gray/dark gray filled regions for the 68% and 95% limit. The other probes are given with their references and typical enclosed radius.

The advantage of our method is that this measurement can be freely reproduced for any structure within the observational boundaries. We have simply isolated a structure in the volume and asks about the mass.

Peculiar velocity field

The second direct result of the analysis is the derivation of the peculiar velocity field for the covered volume. Peculiar velocity field is notoriously complicated to get right. Among the reasons, we find:

• large scale correlations leading to high sensitivity to boundary effects
• requirement to have an unbiased total matter density field.
• systematic effect arising from the use of redshifts to derive the tracer positions and their contribution to the mass density (this is so-called Malmquist bias). The tracers have also specific radial selection properties yielding more systematic effects.

Classic methods have most relied on linear perturbation theory of density fluctuations to derive estimators of these fields. The BORG-PM method allows a self-consistent derivation of these fields including non-linearities. This allows for the first time to have a model of completely non-linear fields like

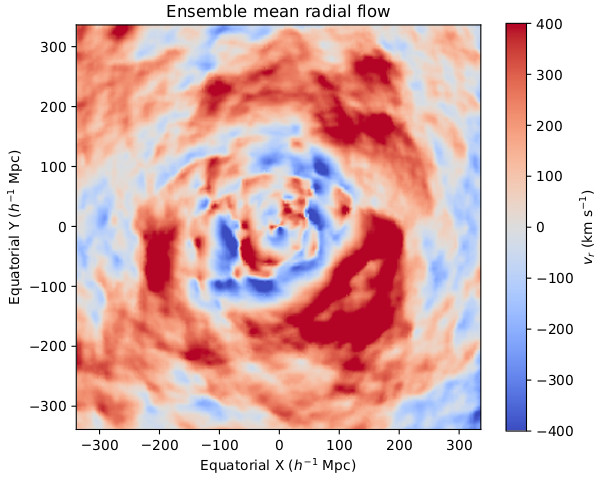Peculiar velocity field picture

The Future

Some other applications are showcases in the paper (e.g. density anomalies, velocity field vorticity). We have only scratched the surface of the possibilities opened by this kind of inference. We invite the interested reader to have a closer look at the article and see recent related work, notably on the fifth work gravity and Alcock Pasczyński effects.

References

• J. Jasche & G. Lavaux, 2019, A&A, 625, A64, arxiv 1806.11117

Authored by G. Lavaux, J. Jasche
Post identifier: /method/borgpm